For univariate data
- Software Method Coefficient Of Skewness
- Coefficient Of Variation Calculator
- Coefficient Of Skewness Formula
- Excel Coefficient Of Skewness
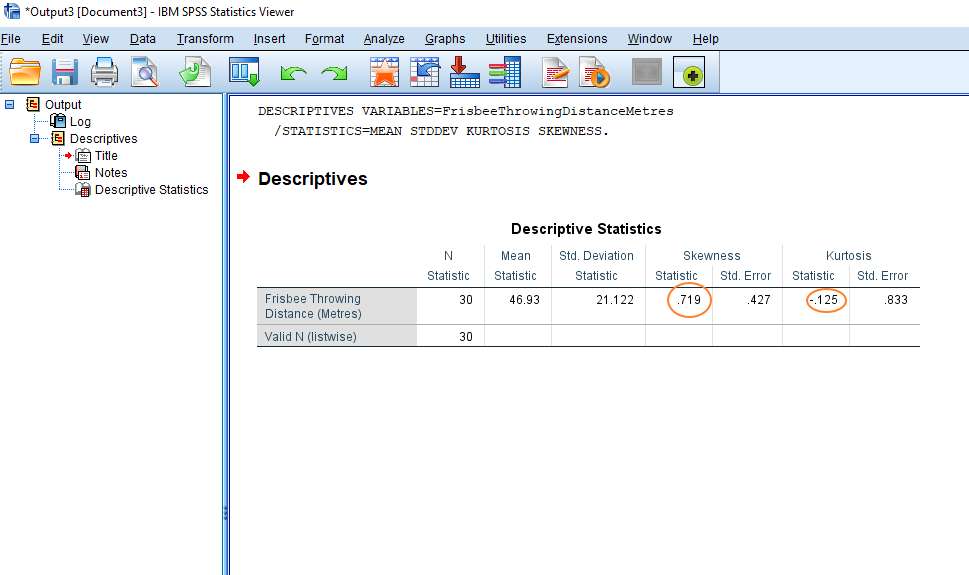
A more complex method of calculating it is the 3rd moment coefficient of skewness. This is what most software programs use. For a perfectly symmetrical curve, such as a normal distribution, skewness is 0. If you look at a curve that is skewed, the mean will appear to be in the tail, the median will be in the middle and the mode will be in the.
, Y- 'Excess coefficient', Encyclopedia of Mathematics, EMS Press, 2001 1994 Kurtosis calculator; Free Online Software (Calculator) computes various types of skewness and kurtosis statistics for any dataset (includes small and large sample tests). Kurtosis on the Earliest known uses of some of the words of mathematics.
- Let me know in the comments if you have any questions on Pearson's coefficient of skewness calculator for grouped data with examples and your thought on this article. Categories All Calculators, Descriptive Statistics, Statistics, Statistics-Calc Tags coefficient of skewness, descriptive statistics, skewness Post navigation.
- Jun 20, 2019 Skewness is a measure of symmetry, or more precisely, the lack of symmetry. A distribution, or data set, is symmetric if it looks the same to the left and right of the center point. A distribution, or data set, is symmetric if it looks the same to the left and right of the center point.
- [ g_{1} = frac{sum_{i=1}^{N}(Y_{i} - bar{Y})^{3}/N} {s^{3}} ]
The above formula for skewness is referred to as the Fisher-Pearsoncoefficient of skewness. Many software programs actually compute theadjusted Fisher-Pearson coefficient of skewness
- [ G_{1} = frac{sqrt{N(N-1)}}{N-2} frac{sum_{i=1}^{N}(Y_{i} - bar{Y})^{3}/N} {s^{3}} ]
The skewness for a normal distribution is zero,and any symmetric data should have a skewness near zero. Negative valuesfor the skewness indicate data that are skewed left and positive values forthe skewness indicate data that are skewed right. By skewed left, wemean that the left tail is long relative to the right tail. Similarly,skewed right means that the right tail is long relative to the left tail.If the data are multi-modal, then this may affect the sign of theskewness.
Some measurements have a lower bound and are skewed right. Forexample, in reliability studies, failure times cannot be negative.
It should be noted that there are alternative definitions of skewness inthe literature. For example, the Galton skewness (also known asBowley's skewness) is defined as
- [ mbox{Galton skewness} = frac{Q_{1} + Q_{3} -2 Q_{2}}{Q_{3} - Q_{1}} ]
The Pearson 2 skewness coefficient is defined as
- [ S_{k_2} = 3 frac{(bar{Y} - tilde{Y})}{s} ]
There are many other definitions for skewness that will not bediscussed here.
View and print this webpage as a pdf file.
What is it?
Flood frequency analyses are used to predict design floods for sites along a river. The technique involves using observed annual peak flow discharge data to calculate statistical information such as mean values, standard deviations, skewness, and recurrence intervals. These statistical data are then used to construct frequency distributions, which are graphs and tables that tell the likelihood of various discharges as a function of recurrence interval or exceedence probability.
Flood frequency distributions can take on many forms according to the equations used to carry out the statistical analyses. Four of the common forms are:
- Gumbel Distribution
Each distribution can be used to predict design floods; however, there are advantages and disadvantages of each technique. Click on the above links to learn more about each technique. According to the U.S. Water Advisory Committee on Water Data (1982), the Log-Pearson Type III Distribution is the recommended technique for flood frequency analysis. Therefore, this analysis is examined in detail here with a step-by-step tutorial.
Log-Pearson Type III Distribution
What is it?
The Log-Pearson Type III distribution is a statistical technique for fitting frequency distribution data to predict the design flood for a river at some site. Once the statistical information is calculated for the river site, a frequency distribution can be constructed. The probabilities of floods of various sizes can be extracted from the curve. The advantage of this particular technique is that extrapolation can be made of the values for events with return periods well beyond the observed flood events. This technique is the standard technique used by Federal Agencies in the United States.
How is it calculated? Microsoft office for mac product key 2011.
The Log-Pearson Type III distribution is calculated using the general equation:
where x is the flood discharge value of some specified probability, is the average of the log x discharge values, K is a frequency factor, and is the standard deviation of the log x values. The frequency factor K is a function of the skewness coefficient and return period and can be found using the frequency factor table. The flood magnitudes for the various return periods are found by solving the general equation. The mean, variance, and standard deviation of the data can be calculated using the two formulas below.

and
| or |
Next, the skewness coefficient Cs can be calculated as follows:
where n is the number of entries, x the flood of some specified probability and is the standard deviation. Excel functions can also be used to calculate the variance (=VAR( ) ), standard deviation (=STDEV( ) ), and skewness coefficient (=SKEW( ) ).
Limbo for mac os x. The skewness estimate (Cs) computed using the equation above is called the station estimate, meaning that the estimate incorporates data values only from the gaging station of interest.
Error and bias in the skewness estimate increase as the number of observations (n) decreases. The 'Bulletin 17B method' recommended by the Interagency Advisory Committee on Water Data (IACWD) uses a generalized estimate of the coefficient of skewness, Cw (for instantaneous peak flow data only), based on the equation:
Cw = WCs + (1-W)Cm
where W is a weighting factor, Cs is the coefficient of skewness computed using the sample data, and Cm is a regional skewness, which is determined from a map.
The weighting factor W is calculated to minimize the variance of Cw, where
Determination of W requires knowledge of variance of Cm [V(Cm)] and variance of Cs[V(Cs)]. V(Cm) has been estimated from the map of skew coefficients for the United States as 0.302 (IACWD, 1982). This simplifies the denominator of the above equation by substitution of 0.302 for V(Cm). Dragon nest for mac os.
The variance of the station skew Cs for log Pearson type 3 random variables can be obtained from the results of Monte Carlo experiments by Wallis et al. (1974). They showed that
where
Software Method Coefficient Of Skewness
A = -0.33 + 0.08 | Cs| if | Cs | 0.90 or
A = -0.52 + 0.30 | C s | if | C s | > 0.90,
B = 0.94 - 0.26 | C s | if | C s | 1.50 or
B = 0.55 if | C s | > 1.50
in which | C s | is the absolute value of the station skew (used as an estimate of population skew) and n is the record length in years.
The coefficient K is then found using tabulated values according to Cw and the return period for each discharge.
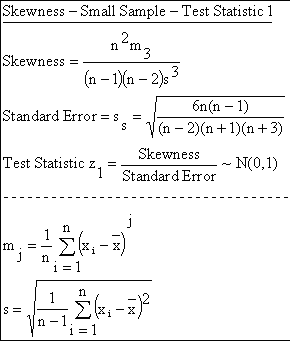
- [ g_{1} = frac{sum_{i=1}^{N}(Y_{i} - bar{Y})^{3}/N} {s^{3}} ]
The above formula for skewness is referred to as the Fisher-Pearsoncoefficient of skewness. Many software programs actually compute theadjusted Fisher-Pearson coefficient of skewness
- [ G_{1} = frac{sqrt{N(N-1)}}{N-2} frac{sum_{i=1}^{N}(Y_{i} - bar{Y})^{3}/N} {s^{3}} ]
The skewness for a normal distribution is zero,and any symmetric data should have a skewness near zero. Negative valuesfor the skewness indicate data that are skewed left and positive values forthe skewness indicate data that are skewed right. By skewed left, wemean that the left tail is long relative to the right tail. Similarly,skewed right means that the right tail is long relative to the left tail.If the data are multi-modal, then this may affect the sign of theskewness.
Some measurements have a lower bound and are skewed right. Forexample, in reliability studies, failure times cannot be negative.
It should be noted that there are alternative definitions of skewness inthe literature. For example, the Galton skewness (also known asBowley's skewness) is defined as
- [ mbox{Galton skewness} = frac{Q_{1} + Q_{3} -2 Q_{2}}{Q_{3} - Q_{1}} ]
The Pearson 2 skewness coefficient is defined as
- [ S_{k_2} = 3 frac{(bar{Y} - tilde{Y})}{s} ]
There are many other definitions for skewness that will not bediscussed here.
View and print this webpage as a pdf file.
What is it?
Flood frequency analyses are used to predict design floods for sites along a river. The technique involves using observed annual peak flow discharge data to calculate statistical information such as mean values, standard deviations, skewness, and recurrence intervals. These statistical data are then used to construct frequency distributions, which are graphs and tables that tell the likelihood of various discharges as a function of recurrence interval or exceedence probability.
Flood frequency distributions can take on many forms according to the equations used to carry out the statistical analyses. Four of the common forms are:
- Gumbel Distribution
Each distribution can be used to predict design floods; however, there are advantages and disadvantages of each technique. Click on the above links to learn more about each technique. According to the U.S. Water Advisory Committee on Water Data (1982), the Log-Pearson Type III Distribution is the recommended technique for flood frequency analysis. Therefore, this analysis is examined in detail here with a step-by-step tutorial.
Log-Pearson Type III Distribution
What is it?
The Log-Pearson Type III distribution is a statistical technique for fitting frequency distribution data to predict the design flood for a river at some site. Once the statistical information is calculated for the river site, a frequency distribution can be constructed. The probabilities of floods of various sizes can be extracted from the curve. The advantage of this particular technique is that extrapolation can be made of the values for events with return periods well beyond the observed flood events. This technique is the standard technique used by Federal Agencies in the United States.
How is it calculated? Microsoft office for mac product key 2011.
The Log-Pearson Type III distribution is calculated using the general equation:
where x is the flood discharge value of some specified probability, is the average of the log x discharge values, K is a frequency factor, and is the standard deviation of the log x values. The frequency factor K is a function of the skewness coefficient and return period and can be found using the frequency factor table. The flood magnitudes for the various return periods are found by solving the general equation. The mean, variance, and standard deviation of the data can be calculated using the two formulas below.
and
| or |
Next, the skewness coefficient Cs can be calculated as follows:
where n is the number of entries, x the flood of some specified probability and is the standard deviation. Excel functions can also be used to calculate the variance (=VAR( ) ), standard deviation (=STDEV( ) ), and skewness coefficient (=SKEW( ) ).
Limbo for mac os x. The skewness estimate (Cs) computed using the equation above is called the station estimate, meaning that the estimate incorporates data values only from the gaging station of interest.
Error and bias in the skewness estimate increase as the number of observations (n) decreases. The 'Bulletin 17B method' recommended by the Interagency Advisory Committee on Water Data (IACWD) uses a generalized estimate of the coefficient of skewness, Cw (for instantaneous peak flow data only), based on the equation:
Cw = WCs + (1-W)Cm
where W is a weighting factor, Cs is the coefficient of skewness computed using the sample data, and Cm is a regional skewness, which is determined from a map.
The weighting factor W is calculated to minimize the variance of Cw, where
Determination of W requires knowledge of variance of Cm [V(Cm)] and variance of Cs[V(Cs)]. V(Cm) has been estimated from the map of skew coefficients for the United States as 0.302 (IACWD, 1982). This simplifies the denominator of the above equation by substitution of 0.302 for V(Cm). Dragon nest for mac os.
The variance of the station skew Cs for log Pearson type 3 random variables can be obtained from the results of Monte Carlo experiments by Wallis et al. (1974). They showed that
where
Software Method Coefficient Of Skewness
A = -0.33 + 0.08 | Cs| if | Cs | 0.90 or
A = -0.52 + 0.30 | C s | if | C s | > 0.90,
B = 0.94 - 0.26 | C s | if | C s | 1.50 or
B = 0.55 if | C s | > 1.50
in which | C s | is the absolute value of the station skew (used as an estimate of population skew) and n is the record length in years.
The coefficient K is then found using tabulated values according to Cw and the return period for each discharge.
Coefficient Of Variation Calculator
For a more detailed description of this method, please refer to the following text:
Bedient, Philip B. and Wayne C. Huber. Hydrology and Floodplain Analysis. Prentice-Hall, Inc., Upper Saddle River, 2002.
What does this particular information tell you about your river?
The Log-Pearson Type III distribution tells you the likely values of discharges to expect in the river at various recurrence intervals based on the available historical record. This is helpful when designing structures in or near the river that may be affected by floods. It is also helpful when designing structures to protect against the largest expected event. For this reason, it is customary to perform the flood frequency analysis using the instantaneous peak discharge data. However, the Log-Pearson Type III distribution can be constructed using the maximum values for mean daily discharge data. A tutorial and example is supplied for both instantaneous and mean daily data.
Coefficient Of Skewness Formula
Tutorial | Example | Tutorial | Example |
| (instantaneous peak flows) | (maximum mean daily discharge) |
Excel Coefficient Of Skewness
Home | Navigation Tips | Preliminary Estimations | Data Manipulation | Analysis Techniques |

